
Table 14 displays the observed minimum and maximum values along with the limits to determine outliers using the quartile rule for each of the variables in the subsample of n=10 participants. Are there outliers in any of the variables? Which statistics are most appropriate to summarize the average or typical value and the dispersion? Table 13 - Summary Statistics on n=10 Participants Table 13 displays the means, standard deviations, medians, quartiles and interquartile ranges for each of the continuous variables in the subsample of n=10 participants who attended the seventh examination of the Framingham Offspring Study. The best summary of a typical diastolic blood pressure is the mean (in this case 71.3) and the best summary of variability is given by the standard deviation (s=7.2). The diastolic blood pressures range from 62 to 81. Outliers are values below Q 1-1.5(Q 3-Q 1) or above Q 3+1.5(Q 3-Q 1) or equivalently, values below Q 1-1.5 IQR or above Q 3+1.5 IQR. A very popular method is based on the following: There are several methods for determining outliers in a sample. When there are outliers in a sample, the median and interquartile range are used to summarize a typical value and the variability in the sample, respectively. When there are no outliers in a sample, the mean and standard deviation are used to summarize a typical value and the variability in the sample, respectively. The same approach is used in the upper half to determine the third quartile ((77+81)/2=79). There are 4 values in the lower half, the first quartile is the mean of the 2 middle values in the lower half ((64+64)/2=64).

When the sample size is 9, the median is the middle number 72. The quartiles are determined in the same way looking at the lower and upper halves, respectively. The median and quartiles are indicated below.įigure 10 - Interquartile Range with Odd Sample Size
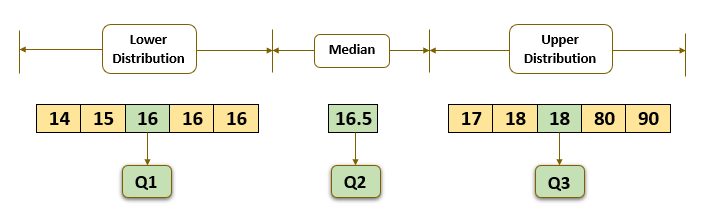
When the sample size is odd, the median and quartiles are determined in the same way. Suppose in the previous example, the lowest value (62) were excluded, and the sample size was n=9. There are 5 values below the median (lower half), the middle value is 64 which is the first quartile. There are 5 values above the median (upper half), the middle value is 77 which is the third quartile. The interquartile range is 77 – 64 = 13 the interquartile range is the range of the middle 50% of the data. The interquartile range is defined as follows:įor the sample (n=10) the median diastolic blood pressure is 71 (50% of the values are above 71, and 50% are below). The quartiles can be determined in the same way we determined the median, except we consider each half of the data set separately.įigure 9 - Interquartile Range with Even Sample Size When a data set has outliers, variability is often summarized by a statistic called the interquartile range, which is the difference between the first and third quartiles. The first quartile, denoted Q 1, is the value in the data set that holds 25% of the values below it. The third quartile, denoted Q 3, is the value in the data set that holds 25% of the values above it. The quartiles can be determined following the same approach that we used to determine the median, but we now consider each half of the data set separately. When a data set has outliers or extreme values, we summarize a typical value using the median as opposed to the mean.


 0 kommentar(er)
0 kommentar(er)
